IAP 1998, Presentation 6 :

FRANK LIGTERINK

The Netherlands Institute for Cultural Heritage

DIFFERENT PASSIVE SAMPLING SYSTEMS FROM A PHYSICAL POINT OF VIEW

Figure 1) Three types of passive samplers designed to measure formaldehyde concentrations in air: a)plain impregnated paper b)tube, c) commercial badge.

Various types of damage on art objects, such as corrosion of metals and certain types of salt-efflorescence, are caused by indoor air pollutants. Measuring pollution concentration levels in museum air is an important tool in controlling this problem. Passive samplers seem best suited for this task(Figure 1). They can be produced and analysed at relatively low costs. They can be located even in small volumes like boxes or showcases by properly instructed museum personnel, and sent back by mail to be analysed at the lab.

In recent years several conservation analytical labs did work to adapt and improve existing passive sampling methods in order to provide cheap and reliable method for museums to monitor concentration levels of small organic acids and aldehydes. At the present we still have not have developed a satisfactory reliable method to measure formaldehyde in museum air. Both varying test conditions and lab procedures seem to cause deviations in the test results.

Theoretically the total uptake of a sampler D M (g) should depend in a simple linear way on the ambient concentration of pollutant C₀,(g/cm³) and the exposure time D t(s).

(1)                

The coefficient of proportionality is called the sampling rate S (cm³/s). It is a measure for the speed of the sampler type and should depend only on the geometry of the sampler. In this paper expressions for theoretically expected sampling rates for two different types of formaldehyde samplers are derived.

Figure 2a) Time evolution of diffusion profile into a diffusion tube immediately after exposure. Subsequent tubes show the profile in the tube for every 5 seconds. After 1 minute the profile no longer changes, it has reached a steady state.

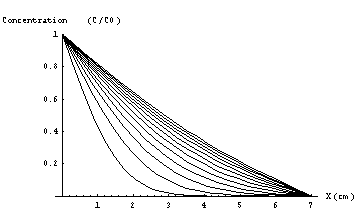
Figure 2b) These 12 curves represent the concentration profiles shown in Figure 2a. Note that after 1 minute the concentration profile has almost reached the steady state.

When a sampler is placed in a large volume, say a showcase with a certain ambient concentration of formaldehyde, the active material from the sampler will start to absorb formaldehyde from the surrounding air. As a result the air directly adjacent to the active material will depleted with formaldehyde . If the binding reaction between formaldehyde and absorbent is fast the concentration directly above the active surface can be considered zero. Every time a formaldehyde molecule reaches the active surface it will be absorbed by it directly. Soon after the first layer of air directly above the absorbent has been depleted subsequent layers will also find their concentrations reduced. Due to the concentration differences at different distances from the active surface a diffusive flow of formaldehyde towards the absorbent will occur. Only after a few minutes [1] a steady-state situation will occur in which the continuing absorption of formaldehyde at the active surface is balanced by a diffusive flow of formaldehyde from the surrounding air towards the surface(Figure 2a, 2b).

We may conclude that the uptake rate of a sampler is limited due to air above the sampler surface. All molecules of formaldehyde that reach the active surface have travelled trough the air above it. Their effective speed is limited trough many collisions with air molecules. For this reason the uptake rate of a sampler is determined by shape of the air volume above the active surface.

Calculation of the theoretical uptake rate of a sampler proceeds in two steps: 1) determine the shape of the steady-state concentration profile above the active surface, 2)calculate the total diffusive flow of formaldehyde due to this concentration profile. Both calculations can be understood from basic principles of diffusion theory.

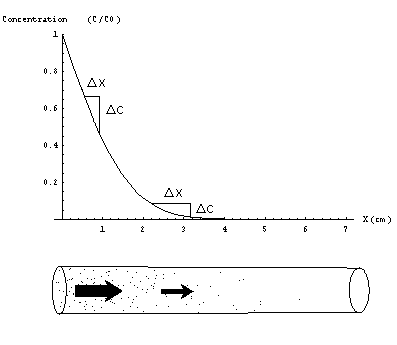
Figure 3) During the first minute of exposure the concentration profile in the tube is more steep at the opening than deeper in the tube. Shown here is the profile after 5 seconds. As a result of Fick's Law the mass flow is larger at the opening than deeper inside.

The steady-state concentration profile above each sampler and the resulting uptake rate are predicted by diffusion theory. Although the precise calculation of diffusion problems can sometimes be rather complicated, the basic principles of diffusion theory are straightforward and can be stated in a few words.

*Fick's law:

The diffusive flow of molecules is driven by a concentration difference. The mass flow per unit area j(g/cm²s) at a certain point in space is directed perpendicular to planes of equal concentration and points towards the area of lower concentration. This mass flow per unit area is directly proportional to the difference in concentration D C (g/cm³) per unit distance D x(cm) (Figure 3). This relation is known as Fick's Law:

(2)                 .

The coefficient of proportionality D (cm²/s) is the diffusion coefficient of formaldehyde in air. It's value (0.16 cm² /s) is reported in literature[2].

*Law of mass conservation:

The second principle of diffusion theory is the Law of Mass Conservation. For a steady-state concentration profile by definition the concentration at a given position must remain constant in time. Considering a volume at this location "all that comes in, must go out"(Figure 4).

*Boundary conditions:

The problem is now uniquely defined if these two principles are combined with assumptions on the concentration profile at the boundaries of the air volume under consideration.

1. At large distances away from the active surface the sampler causes no serious depletion. The concentration profile approaches the ambient concentration C₀.

2. At the active surface the concentration remains (close to) zero.

3. At the non-absorbing surfaces of the system there is no mass flow into them. As a result mass flow is parallel to these surfaces. From Fick's Law it can be concluded that planes of equal concentration must be perpendicular to the se surfaces.

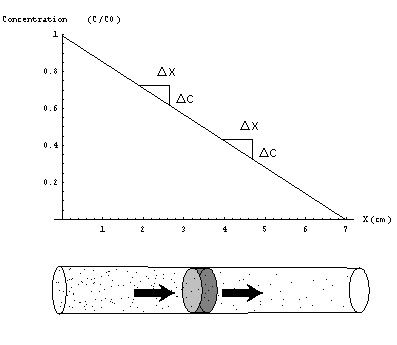
Figure 4) Flow into and out off each volume are equal. This is a necessary condition for all steady state diffusion profiles.

The principles stated above can now be combined to calculate theoretical uptakes for the three samplers. As a first example the uptake rate for the tube type sampler will be derived. Calculation of the uptake rate will proceed according the working scheme set down above. First we will set out to derive the steady-state concentration profile, then the uptake rate will be calculated.

The container part of the tube type sampler consists of an acrylic tube, closed with a cap on the bottom whereon the DNPH-impregnated paper[3] is placed. It has a cross section A of 0.95 cm² and a length L of 7.0 cm. Suppose this tube is exposed to an ambient concentration C₀, what steady state concentration profile will exist in the tube after some minutes?

Several features follow directly from the boundary conditions. 1)The concentration will be zero at the bottom due to the absorbent. 2) Due to its length the uptake rate of the tube sampler is low and it can be assumed that the concentration at the top of the tube is (close to) the ambient concentration C₀. 3) All planes of equal concentration will be perpendicular to the side of the tube.

These conditions suggest a concentration profile consisting of a set of parallel planes of equal concentration. The plane with highest concentration C₀ is located at the top of the tube, inwards the concentration decreases in some manner so that the plane of zero concentration is located at the bottom. It now remains to be shown that concentration can only decrease in a regular linear way in order to be a steady-state concentration profile. Maybe this can be explained best by showing what happens if concentration does not decrease in a regular way towards the bottom. Suppose for instance that concentration profile decreases a lot at the top of the tube and much less at the lower end of the tube(Figure 3). From Fick's law we now know that the mass flow at the top of the tube is larger than the flow at the bottom. As a result the concentration at the middle part of the tube does not stay constant but increases. Only possibility for a concentration profile that stays constant in time is a uniformly decreasing concentration throughout the tube (Figure 4).

Having found the steady state concentration profile we can now proceed to calculate the uptake rate for the tube sampler. The total mass flow per unit area j(g/cm²s) directly above the absorbent material can be found from difference in concentration per unit distance by using Fick's law(2). In this special case the local difference in concentration per unit length is equal to the difference in concentration over the complete tube.

(3)                

The total mass uptake D M(g) of the tube sampler can now be found multiplying the mass flow per unit area j(g/cm²s) with the cross section area of the bottom of the tube A(cm²) and the exposure time D t(s).

(4a)                

Using equation 3 the predicted uptake rate for the tube sampler is

(4b)                

With use of the definition (1), the sampling rate S(cm³/s) of the tube sampler can be read off from this result directly.

(5a)                

The numerical value for this specific tube is

(5b)                

The plain paper sampler consists of a rectangular piece of DNPH-impregnated paper with dimensions 0.18 ´ 0.25 cm² , mounted onto a small sheet of polymeric material(PET). An exact calculation of the concentration profile is difficult for this case. In order to avoid complicated mathematics a simpler solution to an approximated problem will be presented here.

Suppose the rectangular piece of paper is no longer flat but shaped into a half sphere with an effective radius r_eff (cm) and surface area A(cm²) identical to the original flat surface(Figure 5).

(6)                

This half sphere is placed on a flat surface and exposed to an ambient concentration C₀(g/cm³). After a few minutes a steady state concentration profile will be formed. First step in calculating the uptake rate is to find the shape of the steady state profile.

A concentration profile that is consistent with the boundary conditions has surfaces of equal concentration shaped like concentric spheres around the curved sampler surface. Far away from the sampler the concentration will reach the ambient concentration C₀(g/cm³). Approaching the sampler surface the concentration will decrease to a zero concentration at the surface. Note that the surfaces of the half spheres are oriented perpendicular to the surface underneath, which is consistent with the third boundary condition.

The problem that remains to be solved is the radial concentration dependence. It is clear that in order to obtain a steady state concentration profile, the total mass flow through each spherical surface should be the same for each radius r(cm). In other words, the product of mass flow per unit area j(g/cm² s) at a certain radius r times the surface area of the sphere at that radius should remain constant. Closer to the sampler the spheres are smaller so the mass flow per unit area should be larger. The solution that fits this problem is shown in Figure 5.

(7)                

The mass flow resulting from this (by differentiation) is

(8)                

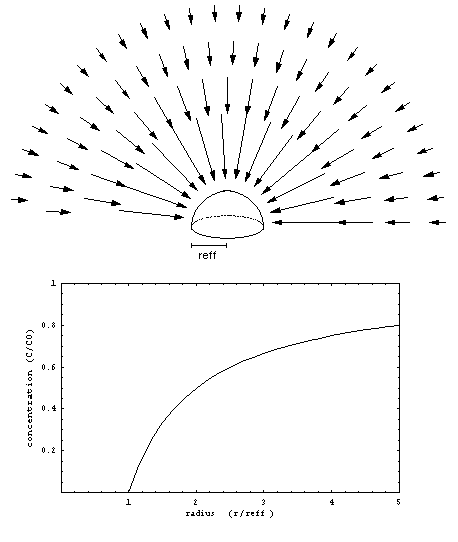
Figure 5) Steady-state concentration profile and resulting diffusive flow towards a spherical surface.x

The mass uptake of the sampler D M(g) can now be predicted multiplying the mass flow j (g/cm²s) at radius r (cm) with the surface area A(cm²) of a sphere with the same radius and with the exposure time D t (s).

(9a)                

(9b)                

As expected that mass transferred does not depend on the radius r(cm) of the sphere.

(9c)                

The sampling rate S(cm³/s) simply depends on the effective radius r_eff(cm) and the diffusion coefficient D(cm²/s) of formaldehyde in air.

(10a)                

The numerical value for the discussed type of plain paper sampler is

(10b)                 .

Both calculated sampling rates (results 5b and 10b) are derived from plain theory and are based on various assumptions. Comparison with experimental data is needed to confirm if these assumptions are justified.

Footnotes

[1] Calculations show that the so-called delay time t (s) needed to reach a steady state situation for a specific sampler type depends on the diffusive length L(cm) of the sampler and the diffusion coefficient D(cm²/s)of the pollutant in air, is of the order of L²/D .

[2] Kring, E.V.,Thornley, G.D., Dessenberger, C.,Lautenberger, W.J., Ansul, G.R., Am. Ind. Hyg. Assoc. J., 43 (1982) 786-795.